Cách chứng minh tứ giác là một hình vuông có ví dụ chi tiết, dễ hiểu
Chứng minh tứ giác là một hình vuông là tri thức căn bản trong hình học cấp THCS. Bài viết sau sẽ chỉ dẫn cách chứng minh một tứ giác là hình vuông với tỉ dụ minh họa đơn giản, dễ hiểu, bám sát chương trình học, mời bạn cùng theo dõi!
1. Hình vuông là gì?
Hình vuông là hình tứ giác có 4 góc vuông và 4 cạnh bằng nhau.

Tứ giác có 4 góc vuông và 4 cạnh bằng nhau là hình vuông
Để hiểu rõ hơn về định nghĩa hình vuông, mời bạn tham khảo bài viết Hình vuông là gì? .
2. thuộc tính hình vuông
Hình vuông là một tứ giác có đầy đủ toàn bộ tính chất của hình chữ nhật và hình thoi. Để xem chi tiết các thuộc tính của hình vuông mời bạn tham khảo bài viết Tình chất của hình vuông .
Hình vuông có đầy đủ ắt tính chất của hình chữ nhật và hình thoi
3. Dấu hiệu nhận biết hình vuông
Hình thoi có một góc vuông hoặc hình chữ nhật có hai cạnh kề bằng nhau là dấu hiệu để nhận biết tứ giác đó là hình vuông.
Để xem chi tiết và đầy đủ các dấu hiệu nhận biết hình vuông mời bạn tham khảo bài viết Dấu diệu nhận biết hình vuông .

Dấu hiệu nhận biết hình vuông
4. Các công thức liên can tới hình vuông
Công thức tính diện tích hình vuông
Diện tích hình vuông bằng bình phương cạnh của hình vuông. Nói cách khác, muốn tính diện tích hình vuông, ta lấy số đo một cạnh nhân với chính nó.
- Công thức : S = a x a = a^2.
- Trong đó :
+ a : Độ dài 1 cạnh của hình vuông.
+ S : Diện tích hình vuông.

Diện tích hình vuông bằng bình phương cạnh của hình vuông
Để hiểu rõ hơn về công thức tính diện tích hình vuông mời bạn tham khảo Công thức tính diện tích hình vuông .
Công thức tính chu vi hình vuông
Chu vi hình vuông bằng tổng độ dài 4 cạnh hay nói cách khác chu vi hình vuông bằng 4 lần độ dài một cạnh của hình vuông.
- Công thức : P = a x 4.
- Trong đó :
+ a : Độ dài 1 cạnh của hình vuông.
+
P
: Chu vi hình vuông.

Chu vi hình vuông bằng tổng độ dài 4 cạnh của một hình vuông
Để hiểu rõ hơn về công thức tính chu vi hình vuông mời bạn tham khảo Công thức tính chu vi hình vuông đầy đủ .
Công thức tính đường chéo hình vuông
1 đường chéo hình vuông sẽ chia hình vuông thành hai phần có diện tích bằng nhau chính là 2 tam giác vuông cân, như vậy đường chéo hình vuông chính là cạnh huyền của 2 tam giác vuông cân đó.
- Công thức : D = a√2.
- Trong đó :
+ a : Độ dài 1 cạnh hình vuông.
+ D : Độ dài đường chéo.

Đường chéo hình vuông chính là cạnh huyền của 2 tam giác vuông cân tạo thành hình vuông
Để hiểu rõ hơn về công thức tính đường chéo hình vuông mời bạn tham khảo bài viết Công thức tính đường chéo hình vuông .
Công thức tính cạnh hình vuông
Bạn có thể dễ dàng tính được cạnh hình vuông khi biết chu vi, diện tích hoặc độ dài đường chéo của hình vuông đó.
- Công thức tính cạnh khi biết chu vi : a = P/4.
- Công thức tính cạnh khi biết diện tích : a = √S.
- Công thức tính cạnh khi biết đường chéo : a = D/√2.
- Trong đó :
+ S : Diện tích hình vuông.
+ P : Chu vi hình vuông.
+ D : Độ dài đường chéo.
+ a : Độ dài 1 cạnh hình vuông.

Công thức tính cạnh hình vuông
Để biết chi tiết công thức tính cạnh hình vuông mời bạn xem ngay bài viết Công thức tính cạnh hình vuông và bài tập có lời giải siêu chi tiết .
5. Cách chứng minh tứ giác là hình vuông
Cách 1: Hình chữ nhật có 2 cạnh kề bằng nhau
Dấu hiệu nhận biết : Hình chữ nhật có 2 cạnh kề bằng nhau là hình vuông.
Để chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có 2 cạnh kề bằng nhau ta thực hiện như sau:
- Chứng minh tứ giác đó là hình chữ nhật.
- Chứng minh tứ giác đó có 2 cạnh kề bằng nhau.
ví dụ : Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC chúng cắt AB, AC theo thứ tự ở M và N. Tứ giác MNGH là hình gì? Vì sao?
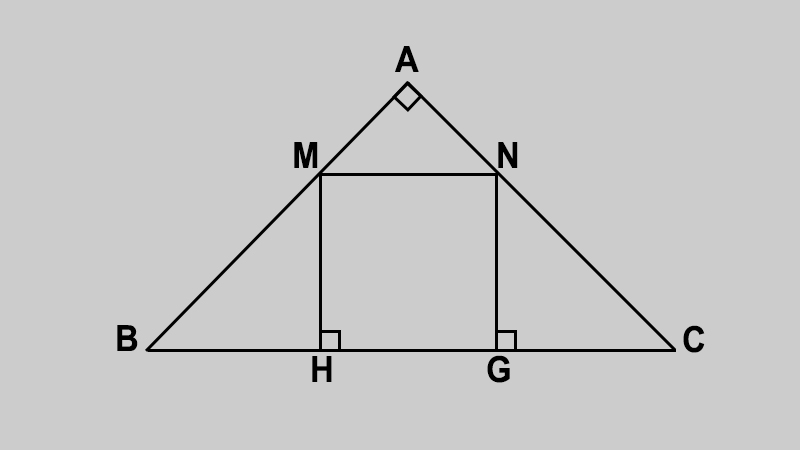
Hình ảnh minh họa cho đề bài

Bài giải cách chứng minh 1
Cách 2: Hình chữ nhật có đường chéo là phân giác
Dấu hiệu nhận biết : Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.
Để chứng minh tứ giác là hình vuông theo dấu hiệu hình chữ nhật có đường chéo là phân giác ta thực hành như sau:
- Chứng minh tứ giác đó là hình chữ nhật.
- Chứng minh tứ giác đó có đường chéo là đường phân giác của một góc.
thí dụ : Cho tam giác ABC vuông tại A, đường phân giác AD. Gọi E, F là chân đường vuông góc kẻ từ D đến AB, AC. Chứng minh rằng tứ giác AEDF là hình vuông.
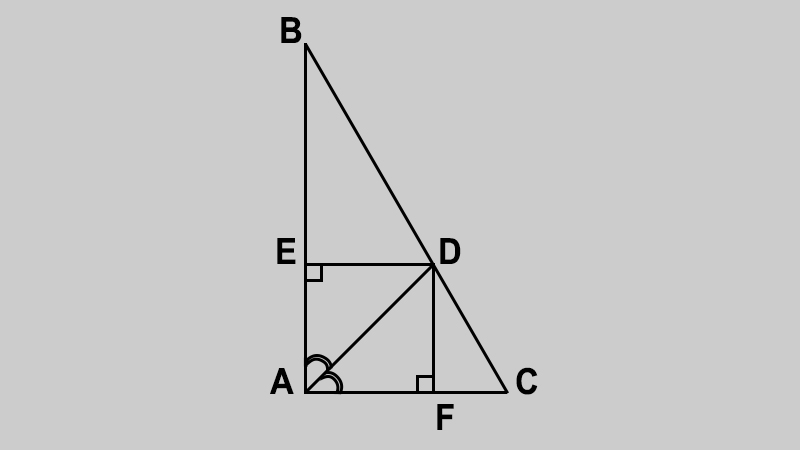
Hình ảnh minh họa cho đề bài

Bài giải cách chứng minh 2
Cách 3: Hình thoi có 1 góc vuông
Dấu hiệu nhận biết : Hình thoi có một góc vuông là hình vuông.
Để chứng minh tứ giác là hình vuông theo dấu hiệu hình thoi có 1 góc vuông ta thực hành như sau:
- Chứng minh tứ giác đó là hình thoi.
- Chứng minh tứ giác đó có 1 góc vuông.
ví dụ : Cho hình vuông ABCD. Trên AB, BC, CD, DA lấy theo trật tự các điểm E, K, P, Q sao cho AE = BK = CP = DQ. Tứ giác EKPQ là hình gì? Vì sao?
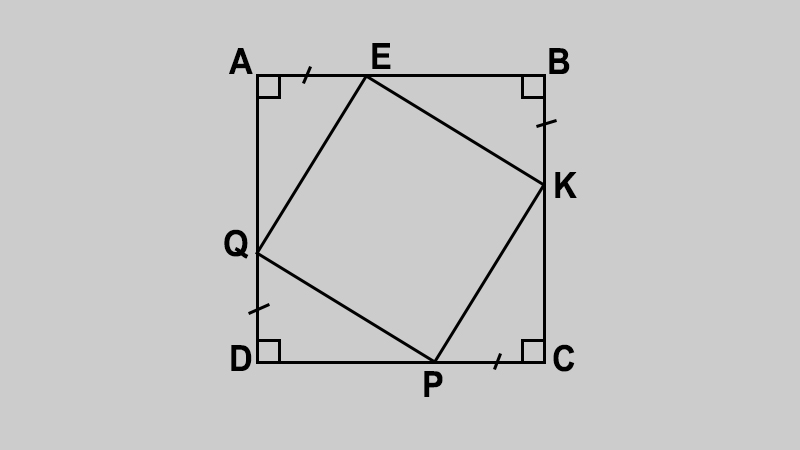
Hình ảnh minh họa cho đề bài

Bài giải cách chứng minh 3
6. Một số lưu ý khi làm bài chứng minh hình vuông
- Nhớ những định nghĩa, tính chất và dấu hiệu nhận biết hình vuông.
- So sánh được sự khác nhau giữa các loại hình.
- Vẽ hình đúng theo đề bài để phục vụ cho việc chứng minh.
- bình thường sau khi đề nghị chứng minh bài tập sẽ có các câu hỏi tính hạnh, bạn nên sử dụng máy tính cầm tay để có kết quả xác thực nhất.

Một trong những lưu ý quan yếu khi làm bài chứng minh hình vuông
Một số mẫu Máy tính cầm tay đang kinh dinh tại Thế Giới Di Động:
-
Máy tính khoa học Thiên Long - Flexio FX680VN Xanh
650.000₫ -
Máy tính khoa học Thiên Long - Flexio FX590VN Xanh Thiên Thanh
460.000₫ -
Máy tính cầm tay Thiên Long - Flexio CAL-06S Xanh Navy
435.000₫ -
Máy tính cầm tay Thiên Long - Flexio CAL-03S Xanh Navy
250.000₫ -
Máy tính cầm tay Thiên Long - Flexio CAL-05P Xanh Navy
190.000₫ -
Máy tính cầm tay Thiên Long - Flexio CAL-02S Xanh Navy
170.000₫
Xem thêm :
mới rồi là cách chứng minh tứ giác là một hình vuông và thí dụ chi tiết, chúc bạn học tốt!
Bài viết can dự
-
Công thức tính thể tích hình hộp chữ nhật có thí dụ đầy đủ, chi tiết
-
Công thức và cách tính đường kính của hình tròn có tỉ dụ minh hoạ
-
Công thức tính đường cao trong tam giác thường, vuông, đều, cân cực dễ
-
Công thức tính đường chéo hình vuông đầy đủ, chi tiết, dễ hiểu
-
Cách tìm x trên máy tính cầm tay cực chuẩn xác khi thi trắc nghiệm
-
Beta là gì? cội nguồn ở đâu? Ý nghĩa của Beta trong một số lĩnh vực



 Có
Có




Không có nhận xét nào: